Soma

I have a boy with Autism, and I am always thinking about teaching tools for him. I have always liked the Soma puzzle by Piet Hein, and decided that that would be a nice puzzle to help exercize Thomas' 3D skills.
I built the puzzle out of wood, and tried it out, but it was just too hard for him. So, I painted the pieces red, yellow, and blue, and have made colored key images.
Because there are seven pieces and only three colors, it is still pretty darn challenging to build the models from the key images, but hopefully it will be possible. If not, I'll paint them seven different colors.
To make the key images, I wrote a program to solve the Soma models. [If Thomas does it that way, too, well, that'll be fine ;-) ] Then, I rendered them using my ambient occlusion texture mapping tool I've been developing for Fast and Furious 3: Tokyo Drift.
The solution program is pretty straightforward. It works by basically trying each block in each position in each orientation, then trying to put in the next block. This will work, but it's really slow. There are a maximum of 24 possible orientations of each block -- some will have fewer unique orientations due to the symmetry of the blocks -- and I'm just trying all 24 every time. Still, the longest solution times were less than a minute on my laptop, and usually less than a second.
A spectacular speedup could be obtained by ensuring that every six-connected region of the unfilled puzzle has a reasonable number of cells; either 3 or 4 modulo 4. I'm sure that if I tested for this after every piece was added, it would speed up the program to a few milliseconds. I've used a similar approach on the pentomino puzzle (A 2D puzzle with the 12 unique 5-piece pentominos filling a 6x10 rectangle, seared into my young brain by the description in Clarke's "Destination Earth". The puzzle-solving scene in that book probably had more to do with me wanting to program computers than anything else.)
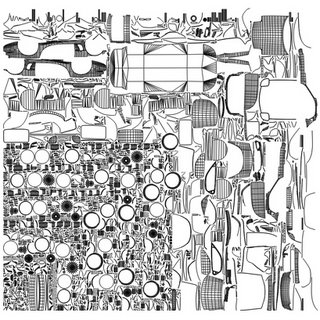
The ambient occlusion calculation takes place in two steps. First, one makes an atlas of the different-colored parts of the model, laying out unique uv-coordinates for each polygon. I've written a very cool program to do automatic atlasing of models, and the uv layouts are often quite pretty. An example of an atlas-ed Mazda RX7 model is shown above. Basically the program works by finding all connected polygonal regions of a model that are relatively flat, projecting them onto the UV plane, and then packing those rectangular UV regions as tightly as possible. Doing this packing tightly will be a subject for a subsequent post.
Once the atlas is created, a ambient-occlusion texture map is created by scan-converting the uv-coordinates, and doing the ambient-occlusion ray-tracing at every pixel. Again, more detail later.

